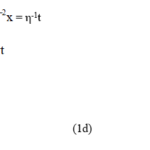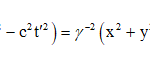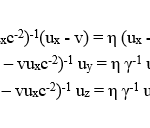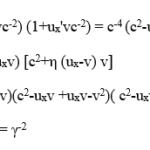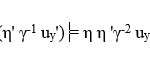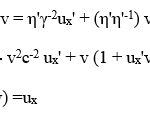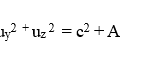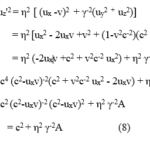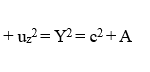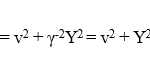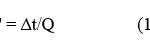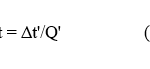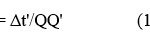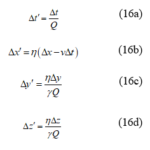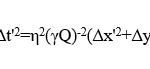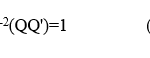J Sci Discov (2019); 4(1):jsd19015; DOI:10.24262/jsd.4.1.19015; Received November 15th, 2019, Revised December 30th, 2019, Accepted January 16th, 2020, Published Februray 18th, 2020.
Relativity theory based directly on the velocity transformation
Robert J. Buenker1,*
1Fachbereich C-Mathematik und Naturwissenschaften, Bergische Universität Wuppertal, Gaussstr. 20, D-42097 Wuppertal, Germany.
* Correspondence: Robert J. Buenker. Fachbereich C-Mathematik und Naturwissenschaften, Bergische Universität Wuppertal, Gaussstr. 20, D-42097 Wuppertal, Germany. E-mail: rjbuenker@gmail.com.
Abstract
The history of the derivations of relativistic space-time transformations is reviewed. Starting with Voigt in 1887, the key assumption was that the speed of light is the same for all observers independent of their state of motion and that of the light source. The fact that fundamentally different transformations have been deduced on this basis can be traced to distinctions that were imposed by their respective authors regarding the relationship between space and time variables. It is pointed out that the same velocity transformation can be derived from each of them by simply dividing each set of spatial variables by the corresponding time coordinate. Many key results of relativity theory, each of which is consistent with all experimental observations made to date, can be obtained on the basis of the velocity transformation alone.
Keywords: Relativistic Velocity Transformation (RVT), Lorentz Transformation (LT), Global Positioning System- Lorentz Transformation (GPS-LT)
Introduction
Experiments carried out in the 19th century indicated something quite unexpected about the speed of light. Michelson and Morley [1] used an interferometer to show, for example, that the speed of light in free space c is the same in all directions, independent of the velocity of the earth at any time during the year. Before that in 1865, Maxwell in his formulation of the theory of electricity and magnetism concluded that the speed of light is the same regardless of the rest frame in which the light source is stationary. Fresnel’s demonstration of the light-drag phenomenon in refractive media a decade earlier had also delivered clear evidence for the constancy of light in free space.
The above results were very confusing to contemporary physicists since they appeared to be inconsistent with one of the sacred tenets of the time, the Galilean space-time transformation. For example, it was strongly held that if a car travels at a speed v of 60 km/h while a train moves in the same direction with a speed of 90 km/h, an observer in the car would find that the train was only moving at 30 km/h. In short, velocities were strictly additive in the prevailing view. Yet, the light-speed measurements led instead to the “shocking” conclusion that c + v = c in this, well-characterized, instance.
Many theories were proposed to explain this discrepancy [2], many of them involving an ill-defined, but universally pervasive, material generally referred to as an ether. These attempts were clearly designed to explain how the light-speed measurements could still be consistent with the Galilean transformation.
Influence of the Voigt Space-time Transformation
In 1887, however, Voigt [3] proposed a different solution to the dilemma by suggesting that the matter could be cleared up by a simple mathematical artifice, whereby the classical transformation would be replaced with one of more general validity. Its main distinguishing feature is that it allows observers in different rest frames to agree on the value of the light speed in free space without giving away the additivity principle of the Galilean transformation for the speeds of objects moving at everyday velocities. The resulting transformation, which connects the three spatial coordinates of a given object, such as the train in the above example, in two different rest frames (x,y,z and x’,y’.z’) with the corresponding time variables t and t’ is given below:
In these equations, v is the relative speed of the two rest frames moving along a mutual x,x’ axis, c is the speed of light in free space (299792458 ms-1), γ = (1-v2c-2)-0.5 and η = (1- vc-2xt-1)-1.
Voigt had several guiding principles in arriving at the above result [3,4]. First, he insisted that eq. (1b) be identical to the classical (non-relativistic) relation that is responsible for the example of the car and train given above. It is given in terms of the elapsed times and distances travelled by the train rather than the speeds measured by the two observers mentioned explicitly in the example. To obtain the desired light-speed constancy relationship, which is not consistent with the classical space-time transformation, Voigt proposed the space-time mixing shown in eq. (1a) to replace the t=t’ equation of the original. This is the first time on record that this concept was ever used. It goes against the long-held view of classical physicists that space and time are fundamentally distinct quantities, one measured with a yard-stick and the other with a clock.
The success with which this purely mathematical exercise achieved its goal can be easily seen by from the following relation obtained by summing the squares of the four equations:
It shows directly that both sides of eq. (2) have the required value of zero if a light wave moving with speed c is the object of the measurements of the two observers.
Nonetheless, from a purely physical standpoint there is a clear deficiency in Voigt’s equations, namely they are in conflict with Galileo’s Relativity Principle (RP). Accordingly, one expects [4] that the inverse of the eqs. (1a-d) can be obtained by simulating the exchange of the positions of the two observers (Galilean inversion) . This is done mathematically by interchanging the primed and unprimed variables and changing the sign of v. In the case of eq. (1c), this procedure leads to the following equation: y=γ-1y’ (note that γ (v) is unchanged by reversing the sign of v). Inserting this value for y in eq. (1c) leads to the nonsensical result of y’= γ-1(γ-1y’)= γ-2y’, proving that this equation is not consistent with the RP.
Historically, the failure of the Voigt transformation was met with an attempt [5] to correct the problem with the RP by simply multiplying each of its four equations on the right-hand side by a common factor, specifically with γ(v). This change leads to the Lorentz transformation (LT), which does indeed satisfy the RP without disturbing the light-speed constancy characteristic of the original. It has only been recognized in the last decade [6,7], however, that the LT also fails to produce a physically viable set of equations. This is because it makes two predictions [8], namely proportional time dilation and remote non-simultaneity, which are mutually contradictory.
A Different Approach Using the Relativistic Velocity Transformation
In the following it will be shown that the Voigt transformation can be used to obtain the true relativistic space-time transformation by first deriving the corresponding velocity transformation. This is easily done by dividing each of the spatial variables x’, y’ and z’ in eqs. (1b-d) by t’ in eq. (1a). To this end is necessary to replace the various quantities with intervals between two points, i.e. Δx= x2-x1, Δx’= x2‘-x1‘, etc. The corresponding velocity components are then obtained as the ratios ux= Δx/Δt, ux‘= Δx’/Δt’, etc. The result is the relativistic velocity transformation (RVT):
It is exactly the same as that obtained from the LT when the analogous procedure is applied to it.
A key question is thus whether the RVT satisfies the RP, even though the Voigt transformation does not. An identity relating the quantities η, η’ and γ, which are found in the RVT as well as the Voigt transformation itself, proves useful in examining this possibility, namely ηη’=γ2 [9]. This is proven below using the respective reciprocals of all three quantities.
Note that eq. (3a) of the RVT has been used to substitute for ux‘.
With the help of eq. (4) it is easily possible to show that the RVT satisfies the RP. The first step is to apply Galilean inversion to eq. (3b), using eq. (4) in the process:
thereby proving that the inverse of eq. (3b) is obtained as a result, as required by the RP.
The analogous procedure can clearly also be used successfully for eq. (3c).
A different approach will be used below to demonstrate that the inverse of eq. (3a) is also obtained by Galilean inversion. Algebraic manipulation of this equation, again using eq. (4) leads to:
thereby showing that the inverse of eq. (3a) also follows as a result of the Galilean inversion. In summary, the RVT satisfies the RP even though the Voigt transformation does not.
It also needs to be shown that the RVT is consistent with the light-speed constancy requirement. Assume that the square of the speed of a given object obtained in the unprimed rest frame (S) is:
According to the RVT of eqs. (3a-c), the corresponding square of the speed of the same object for the observer in S’ is given by:
Therefore, it seen that if an object is measured to have a speed of c by the observer at rest in S, so that A=0 in eq. (7), the observer at rest in S’ will also obtain the same value of c, in accord with the light-speed constancy requirement.
Moreover, the relation in eq. (8) allows one to make several other conclusions. The η2γ-2 factor on its right-hand side is positive definite, at least as long as v<c, as will be assumed in the following discussion. Therefore, if the speed of the object is smaller than c (A<0) for the observer in S, the same will be true for his counterpart at rest in S’. This result has previously been obtained in a different way [10]. It is in agreement with the fact that many attempts have been made experimentally to accelerate an electron to a faster-than-c speed, but without success. If the speed of the object is greater than in one rest frame (A>0), eq. (8) indicates that the corresponding speed in the other rest frame will also exceed c. Again, the same result has previously been obtained in a different way [10].
The relation between velocity component squares in eq. (8) does not appear to have been previously known. It is worthwhile to use it an example to demonstrate both its effectiveness and its compatibility with the RVT result for the same case. Consider an object which moves along the y axis with speed Y from the vantage point of an observer O in the rest frame S:
Since ux=0, η =1 for use in both the RVT and eq. (8). The corresponding sum measured by observer O’ a rest in S’ is therefore obtained from the RVT to be:
According to eq. (9), the constant in eq. (8) has a value of A = Y2 – c2. Substitution thus gives the following result:
which is the same result as obtained first in eq. (10) using the RVT in a more conventional way, as was to be shown.
Newton's Law of Inertia and the Space-time Transformation
Having shown that the RVT satisfies both the RP and the light-speed constancy requirement, attention can now be turned to the possibility of using it to deduce a different space-time transformation to replace both the original Voigt transformation and the LT. This objective can be accomplished quite easily by recalling that such equations are meant to describe purely inertial systems, i.e. objects moving under the absence of unbalanced external forces. That being the case, it would seem highly plausible [11,12] that the properties of inertial clocks remain completely unchanged over time (Law of Causality). This conclusion is clearly quite consistent with Newton’s First Law of Motion (Law of Inertia), which states that inertial systems move indefinitely with constant speed and direction. Beyond this, it needs to be recognized that the rates of two different inertial clocks might not be the same, but in case they do differ, at least their ratio must be constant.
Because of the above state of affairs, the ratio Q of elapsed times Δt and Δt’ measured by two inertial clocks for any event will always be constant as well, i.e.
This equation must also satisfy the RP, and this requirement serves as a condition for inverting it. Applying Galilean inversion to eq. (12) produces the following result:
Substitution for Δt in eq. (12) then leads to eq. (14) below:
On this basis, one concludes that the constant Q’ must be the reciprocal of Q in order for eq. (12) to satisfy the RP. This is an easily understandable result since it simply requires that the inverse ratio of the two elapsed times be the reciprocal of the original defined in eq. (12), i.e.:
The concept of “space-time” has long been thought to be essential in order to guarantee light-speed constancy, but the truth is different. By simply multiplying each of the three equations of the RVT with Δt’ from eq. (12), the result is [13-14]:
This alternative transformation satisfies both the RP and the light-speed requirement, but nonetheless eschews the space-time mixing which was such a departure from classical dogma in the case of both the Voigt transformation of eqs. (1a-d) and the LT. It is obtained from the former by multiplying each of the right-hand sides of its equations by ηQ-1, rather than by γ as in the case of the LT. The relation corresponding to eq. (2) obtained by summing the squares of its four variables is:
showing that light-speed constancy is guaranteed. The condition for satisfying the RP is:
which is also clearly satisfied because of eqs. (4) and (15). The space-time transformation of eqs. (16a-d) has been referred to as the Global Positioning System-Lorentz Transformation (GPS-LT) because it is consistent with procedures used in the navigation system to adjust the rates of atomic clocks on satellites so that they are equal to those of counterparts located on the earth’s surface [13,14]. It was first reported in 2008 for the special case with Q=1 [6].
Conclusion
The relativistic velocity transformation (RVT) is a central component of relativity theory. It can be derived by simple division of the variables in the Voigt transformation of eqs. (1a-d), which was introduced in 1887. It guarantees that the speed of light in free space is the same for any two observers independent of their relative velocity. It also satisfies the RP, as shown by the fact that its inverse can be obtained by Galilean inversion, i.e. the mathematical procedure that simulates the exchange of roles of the two rest frames which are represented in the transformation by interchanging their variables and reversing the sign of their relative speed v.
It is an important fact that the relationship between the associated space and time variables does not need to be specified in order to derive the RVT. To proceed further, it becomes necessary to determine this relationship between space and time. As has been shown, a straightforward means of accomplishing this objective is simply to recognize that the RVT deals with inertial systems, i.e. systems that are moving under the complete absence of unbalanced external forces. It is therefore reasonable to assume that the rates of clocks used to measure the elapsed times needed to specify the velocity components required in the RVT should have perfectly constant rates. This assumption relies on Newton’s Law of Inertia on the hand, and on the Law of Causality on the other. The conclusion is that elapsed times in the two rest frames must be related by eq. (12), in which the variable Q is a constant ratio. It is then easy to show that the space-time transformation of eqs. (16a-d) which results from combining the clock-rate proportionality of eq. (12) with the RVT satisfies both the RP and the light-speed constancy requirement. It is referred to as the Global Positioning System-Lorentz Transformation (GPS-LT) because of its relevance to timing procedures employed in this navigation method. It has the distinct advantage of being internally consistent, unlike both the LT and the earlier Voigt transformation.
Conflict of interest
None
Acknowledgments
None
References
- A. A. Michelson and E. W. Morley, On the Relative Motion of the Earth and the Luminiferous Ether, Am . J. Sci. 34, 333 (1887); L. Essen, Nature, “A New Æther-Drift Experiment,” 175, 793 (1955).
- A. Pais, ‘Subtle is the Lord…’ The Science and Life of Albert Einstein, Oxford University Press, Oxford, 1982, pp. 111-113.
- W. Voigt, Ueber das Doppler’sche Princip, Goett. Nachr., 1887, p. 41.
- R. J. Buenker, Voigt’s conjecture of space-time mixing: Contradiction between non-simultaneity and the proportionality of time dilation, BAOJ Physics 2:27, 1-9 (2017).
- A. Pais, ‘Subtle is the Lord…’ The Science and Life of Albert Einstein, Oxford University Press, Oxford, 1982, pp. 121-123.
- R. J. Buenker, The global positioning system and the Lorentz transformation, Apeiron 15, 254 (2008).
- R. J. Buenker, The Clock Puzzle and the Incompatibility of Proportional Time Dilation and Remote Non-simultaneity, J. App. Fundamental Sci. 4 (1), 6-18 (2016).
- A. Einstein, Zur Elektrodynamik bewegter Körper, Ann. Physik 322 (10), 891 (1905).
- R. J. Buenker, Relativity Contradictions Unveiled: Kinematics, Gravity and Light Refraction, Apeiron, Montreal, 2014, p. 201.
- R. D. Sard, Relativistic Mechanics, W. A. Benjamin, New York, 1970, p. 167.
- R. J. Buenker, Newton’s law of inertia and clock-rate proportionality: Einstein’s historic mistake, BAOJ Physics 3:1, 1-10 (2018).
- R. J. Buenker, Simultaneity and the constancy of the speed of light: Normalization of space-time vectors in the Lorentz transformation, Apeiron 16, 96-146 (2009).
- R. J. Buenker, Relativity Contradictions Unveiled: Kinematics, Gravity and Light Refraction, Apeiron, Montreal, 2014, pp. 55-56.
- R. J. Buenker, GPS-compatible Lorentz transformation that satisfies the Relativity Principle, J. Astrophys.Aerospace Technol. 3, 115, 1-6 (2015).
Copyright
© This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/